Writing Complex Numbers In Polar Form

Hotmath

Home

Polar Form of a Complex Number

The polar form of a complex number is another way to represent a complex number. The form $z = a + b i$ is called the rectangular coordinate form of a complex number.

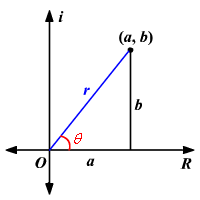
The horizontal axis is the real axis and the vertical axis is the imaginary axis. We find the real and complex components in terms of $r$ and $θ$ where $r$ is the length of the vector and $θ$ is the angle made with the real axis.

From Pythagorean Theorem :

$r^{2} = a^{2} + b^{2}$

By using the basic trigonometric ratios :

$\cos θ = \frac{a}{r}$ and $\sin θ = \frac{b}{r}$ .

Multiplying each side by $r$ :

$r \cos θ = a and r \sin θ = b$

The rectangular form of a complex number is given by

$z = a + b i$ .

Substitute the values of $a$ and $b$ .

$\begin{array}{l} z = a + b i \\ = r \cos θ + (r \sin θ) i \\ = r (\cos θ + i \sin θ) \end{array}$

In the case of a complex number, $r$ represents the absolute value or modulus and the angle $θ$ is called the argument of the complex number.

This can be summarized as follows:

The polar form of a complex number $z = a + b i$ is $z = r (\cos θ + i \sin θ)$ , where $r = | z | = \sqrt{a^{2} + b^{2}}$ , $a = r \cos θ and b = r \sin θ$ , and $θ = \tan^{- 1} (\frac{b}{a})$ for $a > 0$ and $θ = \tan^{- 1} (\frac{b}{a}) + π$ or $θ = \tan^{- 1} (\frac{b}{a}) + 180 °$ for $a < 0$ .

Example:

Express the complex number in polar form.

$5 + 2 i$

The polar form of a complex number $z = a + b i$ is $z = r (\cos θ + i \sin θ)$ .

So, first find the absolute value of $r$ .

$\begin{array}{l} r = | z | = \sqrt{a^{2} + b^{2}} \\ = \sqrt{5^{2} + 2^{2}} \\ = \sqrt{25 + 4} \\ = \sqrt{29} \\ \approx 5.39 \end{array}$

Now find the argument $θ$ .

Since $a > 0$ , use the formula $θ = \tan^{- 1} (\frac{b}{a})$ .

$\begin{array}{l} θ = \tan^{- 1} (\frac{2}{5}) \\ \approx 0.38 \end{array}$

Note that here $θ$ is measured in radians.

Therefore, the polar form of $5 + 2 i$ is about $5.39 (\cos (0.38) + i \sin (0.38))$ .